4.1. Scalability & performance¶
4.1.1. Scalability tests¶

Tests on Franklin
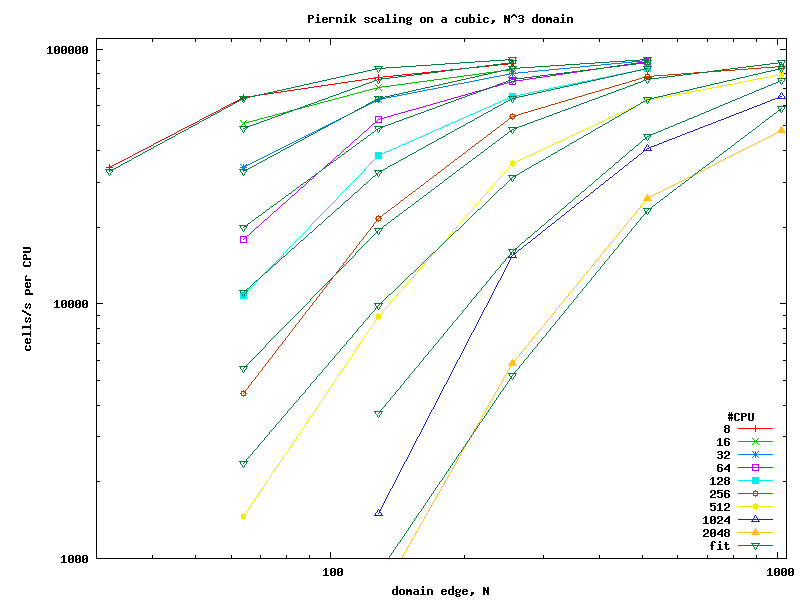
Below are plots showing number of cells per second calculated on each CPU in the first step of a modified Jeans test with isolated boundaries and RBGS relaxation in a 323 to 10243 domain. The tests were run on Franklin at NERSC (Cray XT4: quad-core Opterons 2.3GHz, 2GB RAM/core, !SeaStar2 interconnect with 3D-torus topology).
The ideal scaling would result in a horizontal line at approximately 90000 cells/second/CPU. Lower performance on small domains originates probably mostly in the multigrid module. Note that the first step does not exploit solution recycling in the multigrid, so it is the worst-case for multigrid. Fine tuning of the multigrid and the domain division may also give improvements in performance. In case of N=64 and NCPU=64 it is possible to reduce the walltime of the first step by 1/3.
The time spent on the first step can be approximated as 1.07 10-5 N3/NCPU + 0.0025 N + 2 10-7 NCPU2 seconds. The second term, 0.0025 N, dominates performance degradation for NCPU < 512, it probably comes from the guardcell communication. Does anyone have an idea why it is proportional just to N? The last term is generated by global all-to-all communication and becomes important for NCPU > 1024. Local domain faces would generate a term proportional to (N/NCPU1/3)2, which is not observable here.
Piernik speed with and without multigrid on the same Jeans problem. Multigrid performance drops dramatically for local domains smaller than 323 (coarse level resolution was then 23 - probably too small). Without multigrid the weak scaling (not explicitly shown) looks almost perfect. With multigrid the weak scaling looks good for local domains containing at least 643 cells.

The picture below gives a hint on how many CPUs can give reasonable performance on a given cubic domain.

Pure hydro scaling test: 3D Sedov explosion
The Piernik code was compiled using the Cray compiler with -O3 optimization. Note that some of the Fortran constructs present in r4598 were incompatible with that compiler and thus were commented out. Fortunately, these features were not essential for the Sedov explosion problem.
The problem was run on a 5123 and a 10243 grid on 256, 512, 1024, 2048, 4096 and 8192 CPU cores. The number of used CPU cores is lowest on the right end of the curves and highest on the left end. There were four variants of each run, differing in domain decomposition strategies:
- cartesian decomposition with cartesian communicator
- cartesian decomposition with cartesian communicator and process reordering
- cartesian decomposition with default communicator (MPI_COMM_WORLD)
- non-cartesian (irregular) decomposition with default communicator
It seems that at least for this test and this machine the special communicator, that matches the topology of domain decomposition rarely gives better performance than use of the default communicator. The irregular domain decomposition gives slightly better performance on small domains, because it minimizes the number of guardcells. On large local domains the performance is clearly lower, compared to the other strategies. Partially it could be due to different cache usage, but it is also possible that presence of multiple neighbors on one side may lead to increased waits for the boundary data. The code performance on an irregularly decomposed domain is a non-obvious function of the choice of number of divisions in the Y and Z directions.
The performance of Piernik in this test depends mostly on the size of the local domains and drops about 1/3 of the peak performance when the local domains become as small as 214 cells (e.g. 32 x 32 x 16 cells). At that size with 4 guardcells on each side, the total number of guardcells can match the number of active cells which becomes a considerable overhead. With constant amount of work per CPU core the performance drops typically by less than 10% when resolution is doubled.
4.1.2. Domain Decomposition¶
Dependence of Piernik performance on domain decomposition strategy
Domain decomposition strategy can affect execution time of the Piernik code in several ways: short length in the x direction may increase data cache miss rate because the x-loop is often the inner loop (optimal choice for arrays indexed in (x,y,z)-way) elongated local domains result in increased domain-domain boundary area (and thus increased volume of boundary data, which has to be processed and communicated with MPI). For a periodic, cubic computational domain, divided to Px * Py * Pz local domains, the total amount of boundary data is roughly proportional to Px + Py + Pz.
Benchmarks
In the tables below Px and Py denote pxsize and pysize, pzsize was calculated to get predefined processor count (i.e. Py = 3 and Px = 2 => Pz = 2 for 12-CPU test). The values are the average dWallClock reported during the run.
- advection_test, 963 cells, 12 processors
| Py Px | 1 | 2 | 3 | 4 | 6 | 12 |
|---|---|---|---|---|---|---|
| 1 | 0.90 | 0.74 | 0.73 | 0.74 | 0.80 | 1.04 |
| 2 | 0.72 | 0.68 | 0.70 | 0.82 | ||
| 3 | 0.68 | 0.70 | 0.79 | |||
| 4 | 0.68 | 0.77 | ||||
| 6 | 0.72 | 0.76 | ||||
| 12 | 0.89 |
- advection_test, 1283 cells, 16 processors
| Py Px | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| 1 | 1.61 | 1.31 | 1.25 | 1.46 | 1.97 |
| 2 | 1.30 | 1.16 | 1.23 | 1.49 | |
| 4 | 1.15 | 1.19 | 1.29 | ||
| 8 | 1.27 | 1.37 | |||
| 16 | 1.62 |
Both tests were performed an a single machine equipped with 8 dual-core Opterons 8214, 2.2 GHz, 2x 1 MB L2-cache.
- advection_test, 963 cells, 12 processors
| Py Px | 1 | 2 | 3 | 4 | 6 | 12 |
|---|---|---|---|---|---|---|
| 1 | 1.56 | 1.32 | 1.28 | 1.27 | 1.35 | 1.65 |
| 2 | 1.31 | 1.21 | 1.22 | 1.37 | ||
| 3 | 1.26 | 1.22 | 1.30 | |||
| 4 | 1.26 | 1.29 | ||||
| 6 | 1.32 | 1.33 | ||||
| 12 | 1.56 |
- advection_test, 1923 cells, 12 processors
| Py Px | 1 | 2 | 3 | 4 | 6 | 12 |
|---|---|---|---|---|---|---|
| 1 | 9.53 | 8.54 | 8.33 | 8.38 | 8.66 | 9.95 |
| 2 | 8.48 | 8.13 | 8.18 | 8.65 | ||
| 3 | 8.31 | 8.17 | 8.46 | |||
| 4 | 8.30 | 8.42 | ||||
| 6 | 8.51 | 8.54 | ||||
| 12 | 9.51 |
- advection_test, 1923 cells, 24 processors
| Py Px | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.09 | 4.96 | 4.68 | 4.59 | 4.63 | 4.78 | 5.18 | 6.61 |
| 2 | 4.92 | 4.47 | 4.41 | 4.42 | 4.54 | 5.21 | ||
| 3 | 4.67 | 4.38 | 4.43 | 4.81 | ||||
| 4 | 4.56 | 4.41 | 4.42 | 4.72 | ||||
| 6 | 4.54 | 4.50 | 4.66 | |||||
| 8 | 4.62 | 4.74 | ||||||
| 12 | 4.98 | 5.03 | ||||||
| 24 | 6.08 |
The three above test were performed an a single machine equipped with 8 quad-core Opterons 8354, 2.2 GHz, 4x 512 KB L2-cache, 2 MB L3-cache.
Conclusions
- The execution time depends most on the size of local domain boundaries.
- Division in the x direction degrades performance most significantly.
- Division in the z direction gives slightly better results than division in the y direction.
- The influence od division in the x directions more significant on small domains.
- The size of L2-cache matters a lot.
Regular vs irregular domain decomposition
Intrigued by relatively poor performance of irregular domain decomposition in the scaling tests on an 10243 grid and 256 CPU cores, we performed a number of additional tests with Py and Pz set explicitly. By default, the irregular domain decomposition sets both Py and Pz to 7 in this case. Setting Py and Pz equal to 8 results in an essentially cartesian decomposition (without cartesian communicator), which previously had the performance 219.6 thousands cells per second per CPU. In the left table below we present the performance in thousands cells per second per CPU for a number of (Py, Pz) pairs. The right table presents effective Px. Single value of Px corresponds to topologically cartesian decompositions.
| thousands cells per second per CPU | Px | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Py Pz | 4 | 5 | 6 | 7 | 8 | 9 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 4 | 205.0 | _183.5_ | _186.9_ | 207.3 | 216.2 | 198.2 | 16 | 12-13 | 10-11 | 9-10 | 8 | 7-8 | |
| 5 | 206.2 | 204.6 | 211.0 | 213.8 | 215.5 | _188.4_ | 12-13 | 10-11 | 8-9 | 7-8 | 6-7 | 5-6 | |
| 6 | 209.4 | 193.0 | 214.8 | 190.6 | 216.4 | 201.7 | 10-11 | 8-9 | 7-8 | 6-7 | 5-6 | 4-5 | |
| 7 | 211.1 | 195.3 | 195.2 | 191.7 | 218.2 | 202.8 | 9-10 | 7-8 | 6-7 | 5-6 | 4-5 | 4-5 | |
| 8 | 213.1 | 195.2 | 203.0 | 196.1 | 219.6 | 201.7 | 8 | 6-7 | 5-6 | 4-5 | 4 | 3-4 | |
| 9 | 212.1 | 201.3 | 203.3 | 217.3 | 194.9 | 201.6 | 7-8 | 5-6 | 4-5 | 4-5 | 3-4 | 3-4 | |
As we can see, the performance is generally good at (Py, Pz) corresponding to best cartesian decompositions, such as (8,8), (8,4) and (4,8). Some noncartesian choices also results in excellent performance. There also exists few “unlucky” choices of (Py, Pz), that may lead to performance reductions up to 20% and the default (7,7) can be considered to be one of them.
The load imbalance due to uneven distribution of cells does not exceed 1% in these runs, so it cannot be attributed to observed performance reductions.
4.1.3. 32-bit and 64-bit issues¶
Operating System
- A 32-bit operating system will not allow you to allocate too much memory. You may expect problems with allocation of regular arrays (with error messages) or strange SIGSEGVs on allocation of temporaries when the process size approaches 3 GB. Largest possible domain per thread on a 32-bit system is about 16 Mcells for pure hydro simulations (or about 21 Mcells repeat_step disabled). With multigrid solver the trouble may begin at about 7 Mcells. With PAE-enabled kernel and multi-core CPU you may run larger simulations on a 32-bit system if you use mpirun/mpiexec to run piernik in more threads.
- The performance of the Piernik code may be higher on a 64-bit operating system, e.g. on a Phenom II processor and gfortran 4.6.0 compiler the difference is approximately 10%.
There are no other known issues that are specific to 32- or 64-bit operating systems.
Default integer length
The Piernik code uses 32-bit (4-byte) integers by default. There are certain calculations that may produce overflows with the 32-bit integers and 64-bit integers (kind=8) are declared in some parts of the source code. With deep AMR structures some more issues of this kind are expected. It should be possible to write the code in a way that is compatible with 64-bit integers as the default length. There are certain issues that require some attention:
- All integers that are passed as arguments to the HDF5 library calls and are not HID_T or similar type should be cast to kind=4. This is checked by the compiler.
- All integers that are passed as arguments to the MPI library calls should be cast to kind=4. This is not checked by the compiler because the interface of the MPI library is a bit too flexible (probably for compatibility reasons).
- Integers in calls to other libraries were not investigated yet.
- Enumerators have the default kind=4. It is possible to promote them to kind=8, but it is not guaranteed that every compiler will have necessary flags. It is thus better to leave the enumerators at their default length.
- Current implementation (since r4602 or so) can be compiled with 8-byte integers. Due to not fully resolved issues with length of arguments in MPI calls it runs correctly only in a single process.
- The performance of Piernik with default 4-byte integers is approximately 10% better compared to executable with 8-byte integers (Phenom II CPU, gfortran 4.6.0). That 10% difference is the same on a 32-bit and 64-bit operating system (Linux).

